My attempt at calculating the resulting velocities of two spheres colliding in 3D.
Background
I’m currently working on a physics simulator (called simp). While build the simulator I’m learning that calculating the physics is easy, but detecting and handling collisions is hard!
As an example, the following is code I wrote last week for determining if a sphere and box are touching in 3D (and then attempting to handle the collision if they are). It’s complex and not even fully correct! It doesn’t handle the case of a sphere touching the corner of the box. And it still took me the better part of an entire day (I spent many hours trying to be clever instead of just handling all 6 faces of the box).
if (e1.shape == Shape.Sphere && e2.shape == Shape.Box) {
let radius = (e1 as SphereEntity).radius
let dimensions = (e2 as BoxEntity).dimensions
let boxMax = new Vector3(0, 0, 0)
let boxMin = new Vector3(0, 0, 0)
let sphereMin = new Vector3(0, 0, 0)
var sphereMax = new Vector3(0, 0, 0)
var inBounds = new Vector3(0, 0, 0)
for (let i = 0; i < 3; i++) {
boxMax.set(i, e2.position.at(i) + dimensions.at(i))
boxMin.set(i, e2.position.at(i) - dimensions.at(i))
sphereMax.set(i, e1.position.at(i) + radius)
sphereMin.set(i, e1.position.at(i) - radius)
if (boxMin.at(i) < e1.position.at(i) && e1.position.at(i) < boxMax.at(i)) {
inBounds.set(i, 1)
}
}
for (let i = 0; i < 3; i++) {
if (inBounds.at((i + 1) % 3) == 1 && inBounds.at((i + 2) % 3) == 1) {
if (sphereMin.at(i) > boxMin.at(i) && sphereMin.at(i) < boxMax.at(i)) {
if (!e1.fixed) {
e1.position.set(i, boxMax.at(i) + radius)
e1.velocity.set(i, -e1.velocity.at(i))
}
if (!e2.fixed) {
e2.velocity.set(i, -e2.velocity.at(i))
}
}
if (sphereMax.at(i) < boxMax.at(i) && sphereMax.at(i) > boxMin.at(i)) {
if (!e1.fixed) {
e1.position.set(i, boxMin.at(i) - radius)
e1.velocity.set(i, -e1.velocity.at(i))
}
if (!e2.fixed) {
e2.velocity.set(i, -e2.velocity.at(i))
}
}
}
}
}
Today’s Problem
This weekend I’ve been tackling a different but similar problem.
I’m trying to calculate the resulting velocity vectors of two colliding sphere’s.
It seems like this should be something pretty simple? But I can’t figure out a general rule that accounts for all cases. (If there is one PLEASE comment it down below).
It seems like there’d be an infinite number of solutions? (I know that’s not the case), but if two spheres bounce into each other, it seems reasonable that they could bounce off each other with a number of different velocities. Maybe one ball stops and all the momentum is transfered? Maybe they swap velocities? Maybe they swap velicities proportional to their mass?
This was my attempt to use some math and figure it out.
My Solution
First I started with the conservation of momentum and conservation of energy equations. We know they must be equal at the beginning and end of the collision. (We’re only using kinetic energy since there shouldn’t any change in potential at the point of collision.)
$$ m_{1} v_{1i} + m_{2} v_{2i} = m_{1} v_{1f} + m_{2} v_{2f} $$
$$ \frac{1}{2} m_{1} v_{1i}^2 + \frac{1}{2} m_{2} v_{2i}^2 = \frac{1}{2} m_{1} v_{1f}^2 + \frac{1}{2} m_{2} v_{2f}^2 $$
Since we can calculate the initial momentum \( p*{i} \) and kinetic energy \( K*{i} \), let’s substitute those into our two equations before things get messy:
$$ p*{i} = m*{1} v*{1f} + m*{2} v_{2f} $$
$$ K*{i} = \frac{1}{2} m*{1} v*{1f}^2 + \frac{1}{2} m*{2} v_{2f}^2 $$
Then, we can solve both equations for \( v_{2f} \):
$$ \frac{p*{i} - m*{1} v*{1f}}{m*{2}} = v*{2f} $$ $$ \frac{K*{i} - \frac{1}{2} m*{1} v*{1f}^2}{\frac{1}{2} m*{2}} = v*{2f}^2 $$
Now let’s join them together so we’re only left with \( v_{1f} \).
$$ \frac{ (p*{i} - m*{1} v*{1f}) ^2}{m^2_2} = \frac{K*{i} - \frac{1}{2} m*{1} v*{1f}^2}{\frac{1}{2} m_{2}} $$
The only unknown left is \( v*{1f} \). Bingo! We have both \( v*{1f} \) and \( v_{1f}^2 \), so there will be multiple solutions(?). Let’s simplify:
$$ \frac{ p*{i}^2 - 2 p*{i} m*{1} v*{1f} + m*{1}^2 v*{1f}^2 }{m^22} = \frac{ 2K{i} - m*{1} v*{1f}^2}{ m_{2}} $$
$$ v*{1f}^2 ( m*{2} m*{1}^2 + m^2_2 m*{1}) + v*{1f} (- 2 p*{i} m*{1} m*{2}) + (p*{i}^2 m*{2} - 2 m^22 K{i}) = 0 $$
$$ v*{1f}^2 + v*{1f} \frac{(- 2 p*{i} m*{1} m*{2})}{m*{2} m*{1}^2 + m^2_2 m*{1}} + \frac{p*{i}^2 m*{2} - 2 m^22 K{i}}{m*{2} m*{1}^2 + m^22 m{1}} = 0 $$
What does that mean? Not sure yet. Let’s solve a couple of examples and see what happens.
Two equal balls colliding at equal speed

| \( m_1 \) | \(v_{1i} \) | \( m_2 \) | \( v_{2i} \) | \( p \) | \( K_i \) | \( \frac{(- 2 p*{i} m*{1} m*{2})}{m*{2} m*{1}^2 + m^2_2 m*{1}} \) | \( \frac{p*{i}^2 m*{2} - 2 m^22 K{i}}{m*{2} m*{1}^2 + m^22 m{1}} \) |
|---|---|---|---|---|---|---|---|
| 5 | 5 | 5 | -5 | 0 | 125 | 0 | -25 |
So our derived equation becomes:
$$ v*{1f}^2 + v*{1f} (0) + -25 = 0 $$
$$ v_{1f} = \pm 5 $$
Which makes sense, two objects at equal speed and mass bounce off each other equally.
Two equal mass balls colliding at unequal speeds
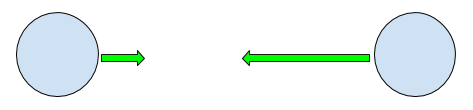
| \( m_1 \) | \(v_{1i} \) | \( m_2 \) | \( v_{2i} \) | \( p \) | \( K_i \) | \( \frac{(- 2 p*{i} m*{1} m*{2})}{m*{2} m*{1}^2 + m^2_2 m*{1}} \) | \( \frac{p*{i}^2 m*{2} - 2 m^22 K{i}}{m*{2} m*{1}^2 + m^22 m{1}} \) |
|---|---|---|---|---|---|---|---|
| 5 | 5 | 5 | -15 | -50 | 625 | 10 | -75 |
$$ v*{1f}^2 + v*{1f} (10) + -75 = 0 $$
So we need to apply the quadratic formula (holy crap, high school math flash back):
$$ v_{1f} = \frac{ -b \pm \sqrt{ b^2 - 4 a c}}{2a} $$
$$ v_{1f} = 5,-15 $$
(Oddly we have two solutions. We’re going to ignore the first solution for a second). Using the conservation of momentum we get velocity of the second ball:
$$ v_{2f} = -15,5 $$
(Ignoring the first solution again). So they swap velocities. Neat!
Why Two Solutions?
At first I was very confused about why there were two solutions, and then I realized, we started this exercise with just two conservation laws, we never “said” they collided. So they could just continue along their current paths and that would satisfy the equations! (But obviously in the real world they collide).
Two unequal balls colliding at equal speed

| \( m_1 \) | \( m_2 \) | \(v_{1i} \) | \( v_{2i} \) | \( p \) | \( K_i \) | \( \frac{(- 2 p*{i} m*{1} m*{2})}{m*{2} m*{1}^2 + m^2_2 m*{1}} \) | \( \frac{p*{i}^2 m*{2} - 2 m^22 K{i}}{m*{2} m*{1}^2 + m^22 m{1}} \) | \( v_{1f} \) | \( v_{2f} \) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 15 | 5 | -5 | -70 | 200 | 8.75 | -68.75 | -13.75 | -3.75 |
| 5 | 15 | 5 | -5 | -50 | 250 | 5.00 | -50.00 | -10.00 | 0.00 |
| 10 | 5 | 15 | -5 | -25 | 312.5 | 2.00 | -35.00 | -7.00 | 3.00 |
So depending on the initial masses, a couple of things can happen.
- When \( m_1 = 1, m_2 = 15\), \( m_1 \) will be pushed back into the reverse direction, and \(m_2 \) will continue pushing ahead.
- When \( m_1 = 5, m_2 = 15\), \( m_1 \) will be pushed back, and \(m_2 \) will stop in place!. How cool!
- When \( m_1 = 10, m_2 ==15\), \(m_1 \) and \(m_2 \) will bounce back in opposite directions.
A bigger ball gives the smaller ball a gentle love tap
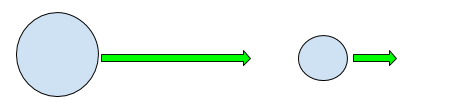
| \( m_1 \) | \(v_{1i} \) | \( m_2 \) | \( v_{2i} \) | \( p \) | \( K_i \) | \( \frac{(- 2 p*{i} m*{1} m*{2})}{m*{2} m*{1}^2 + m^2_2 m*{1}} \) | \( \frac{p*{i}^2 m*{2} - 2 m^22 K{i}}{m*{2} m*{1}^2 + m^22 m{1}} \) |
|---|---|---|---|---|---|---|---|
| 15 | 10 | 5 | 5 | 175 | 812.5 | -17.5 | 75 |
$$ v*{1f} = 10, 7.5 $$ $$ v*{2f} = 5, 12.5 $$
Now that’ weird. There’s two solutions that don’t match the initial conditions. But, we can eliminate one of them. If the bigger ball sneaks up on the little ball, it’s probably not going to jump over the first ball. So we know that \(v*{1f} < v*{2f} \). Only the second solution matches that. Therefore, the first ball transfers some of it’s momentum to the second ball, as expected.
$$ v*{1f} = 7.5 $$ $$ v*{2f} = 12.5 $$
Open Questions
- When the sphere’s give each other a love tap, there’s two solutions. Why doesn’t one of the solutions equal the initial conditions?
Conclusion
Success!
Using only two conservation laws we were able to determine the outcome of two colliding spheres. Technically we only did it in 1D, but as long as you respect the vector math, it should just work in 3D.
I’m going to codify the solutions into simp, I’ll put the results in part 2.