A smaller project involving plotting ionization energy for different effective nuclear charge models.

Overview

Tonights project was from a book I’m reading called “The Oxford Solid State Basics”. In the problem you were supposed to calculate and plot the ionization energy for atoms from hydrogen to Manganese.

The code can be found here:

https://github.com/c0nrad/atomic

Results:

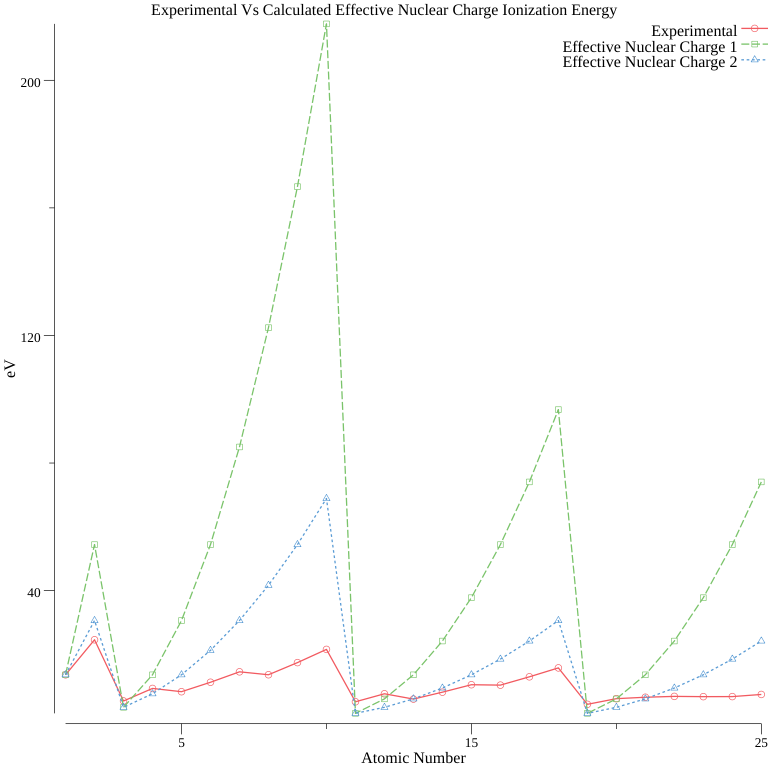
It turns out the calculated ionization energies had the same shape, but overshot the experimental values by quite a bit.

Effective Nuclear Charge

The problem was based around the idea that surprisingly atoms on the left side of the periodic table are larger than the atoms on the right. Even though the atoms on the right have more electrons and protons.

This can be explained by the fact that the inner electrons sort of “shield” the external electrons.

The atoms on the far left have one extra electron in their outer shell. So when the “electrons look in” they see X protons, and X-1 electrons. But, the atoms on the right will see X protons, and X-7 electrons (in the case of florine) since the extra electrons are in the same orbital.

So if we wanted to ionize an electron from an atom, it’d much simpler to pull one of the electrons off the fat atoms (left) than one of the skinner atoms (right).

The project involved calculating this ionization energy.

Calculations

To model the ionization energy, the book recommended using the hydrogen model with effective charge Z.

This makes sense because we modeled the hydrogen atom using the Coloumb potental. So instead of just one electron and one proton, we can say one electron and “effective nuclear charge” protons.

I found this in my trusty Griffiths book:

$$ E_n = -\left[ \frac{m_e}{2\hbar^2} \left( \frac{e^2}{4 \pi \epsilon_0} \right)^2 \right] \frac{1}{n^2} $$

So then we just needed to multiply one of the \( e \)’s by a Z, and calculate the \( n \) for each atom from 1-25.

To calculate the Z two different naive approaches were used:

1. Consider all inner electrons to shield, ignore the electrons in the same shell
2. Consider all inner electrons to shield, and electrons in the same shell to 1/2 shield

Future

It was a fun evening project, but I don’t see myself continuing the project.

If I do, I learned while researching that there’s a set of rules called “Slater’s Rules” for calculating Effective Nuclear Charge that would probably give better results.