c0nrad's c0rner

Learning and learning

Jul 3, 2020 - 6 minute read - quantum computation

Quantum Teleportation Algorithm

This post is split into two parts. The first section is my motivation, and some background on the upgrades I made to my quantum simulator. The second part is implementing the Quantum Teleportation algorithm.

Motivation

Recently I’m been playing more with Quantum Computing.

Quantum Computing fits nicely into my current goals of:

  1. learning more about the universe
  2. learning something practical

A long time ago I built a little Quantum Computer Simulator for a internal company “hackathon”. At the time I worked at a database company, so I implemented Grover’s algorithm. (Grover’s Algorithm can be used to find an element in an unsorted array. Normally you’d have to search every element in the array until you get a match, but using a quantum computer, you can do it significantly faster (supposedly O(Sqrt(N)), but for smaller data sets I was able to do it in one pass. I’ll be talking about Grover’s algorithm at some point in the near future :), see next paragraph).

I decided my next “long term” project will be to build a Quantum Hash Cracking algorithm. After thinking more about it, I’m pretty sure I can do it with Grover’s algorithm. But since it’s a simulated quantum computer, I can only simulate a couple of qubits, I so think I’ll actually be “cracking” CRC4. We’ll see. Maybe if I can get it working I can finagle IBM/GOOG into letting me verify CRC-16 or something on one of their quantum computers.

Upgrades to QRAD

But the quantum hash-cracker is a little ways off. First I want to dust off the old simulator. The old simulator was heavily based on the book Quantum Computing for Computer Scientist. A great book if you have a CS background and want to get your hands dirty.

But, after playing with IBM’s Qiskit, Google’s Cirq and Algassert’s Quirk, and I love how they do certain things. Specifically how they approach circuit building, so I rebuilt part of my simulator. Specifically:

  1. Added “Moments”, a better way to organize gates
  2. Circuit Diagrams, so I can see what the circuits look like
  3. Arbitrary number of Control gates, CCCCCCCCNOT gates
  4. Measure/collapse independent Qubits, previously I could only collapse the entire state
  5. Treat circuit more like a state machine, append a bunch of moments, and then later execute the circuit, or resume execution

Implementing Quantum Teleportation

That algorithm I chose to implement first was Quantum Teleportation. Quantum Teleportation sounds super badass (and it is decently cool), but maybe not “super badass”. The math is pretty cool, and I’m guessing there’s some practical usage that I’m not aware of.

Quantum Teleportation allows you to transfer the state of one qubit, to another qubit. In the classical world, this sounds super lame. But there’s some hurdles in the quantum world that make this difficult, hence why it’s a neat algorithm.

There’s something called No-Cloning Theorem, which states you can’t copy the state of a qubit to another qubit (due to limits on Quantum Information). You also can’t “peek” inside the state of a qubit. The qubit could be in any number of an infinite set of positions, but we can only ask it one single “yes or no” question.

How it works

Alice wants to send Bob the state of one of her qubits. Why? No idea.

And for some reason she can’t just send Bob the Qubit. But they are able to share an Entangled Qubit. (Maybe Eve is able to generate a set of entangled Qubits and send one to Bob and one to Alice).

Alice must then perform some actions both her original qubit and her entangled qubit. After performing the actions she will measure the state of her two qubits (destroying the qubit she wants to transfer).

Alice then sends Bob the results of her measurements. (two classical bits). Using those two classical bits, Bob can construct the original state of Alice’s first Qubit.

The circuits

If you want to see a very neat demo of the algorithm, check out Algassert’s online quantum editor for quantum teleportation.

Here’s my significantly less sexy circuit diagram:

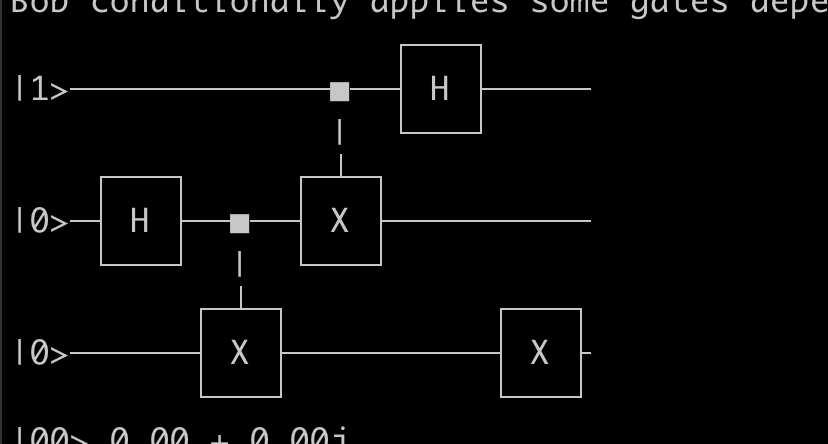
equal speed, equal mass

Code: https://github.com/c0nrad/qrad/blob/master/circuits/teleportation/teleportation.go

The maths

The coolest part of the whole thing (in my opinion) is the maths. Following along in Quantum Computation and Information Theory (supposedly the bible in the field, haven’t finished it yet though, so no opinion yet), there’s a single line that pretty much describes the entire algorithm:

$$ |\psi\rangle = \frac{1}{2} [ |00 \rangle (\alpha|0\rangle + \beta|1\rangle) + |01 \rangle(\alpha|1\rangle + \beta |0\rangle) + |10\rangle (\alpha|0\rangle - \beta|1\rangle) + |11\rangle(\alpha|1\rangle - \beta|0\rangle) ]$$

It can be a little tricky to read. Here’s a cheat sheet.

  • There’s three qubits in this system. The first two belong to Alice, the last to Bob
  • The qubits can be identified by the weird \( |00\rangle, |1\rangle \) symbols.
    • These are called “ket’s” (After Dirac’s Bra-Ket notation, used a lot in quantum mechanics)
    • So the qubits belonging to Alice look like \( |00\rangle, |01\rangle, |10\rangle, |11\rangle \) and the Qubit belonging to Bob look like \( |0\rangle, |1\rangle \)
  • Alice’s qubit that she wanted to transmit started in the state \( \alpha|0\rangle + \beta |1\rangle \), but in this equation the \( \alpha \) and \( \beta \) are on the final qubit (Bob’s qubit), and in four different configurations.
    • Each of the four configurations has an equal probability
  • \( |00\rangle, |01\rangle, |10\rangle, |11\rangle \) are the four states that alice can measure. So, if she measures 0, 1, if means that Bob’s qubit must be in the state \( \alpha|1\rangle + \beta|0\rangle \)
    • This means that Bob needs to invert the \( |1\rangle \) and \(|0\rangle \) to get back Alice’s original state (to invert Bob just needs to apply an X gate to his qubit)

Getting the qubits into the form of that equation isn’t too hard either. It just takes some carefully placed Hadamard and CNOT gates.

After all of that, Alice can transfer a Qubit to Bob! And Bob should have an exact match of the original Qubit alice had.

Difficulties

Things that were more difficult to implement than planned:

  • I can’t tell if I’m being dumb, or thinking about it the wrong way. But constructing the unitary matrixies for each moment is surprisingly complex when there’s “gaps” and multiple CONTROLs.
    • My solution is extremely janky, and I do not trust it. Almost all the time I spent over the last few days was writing an algorithm to generate arbitrary matrixies with an arbitrary number of gaps and control gates. I asked on reddit if anyone knew how to do this, and they said I could Tensor Product the control gates, but I don’t believe that to be true. But something I need to look into, because that would be super nice if I could.
    • (Edit, some more people responded, I can’t use Tensor products. Not going crazy)
  • Collapsing a single qubit. First you have to measure if the qubit should be “1' or “0”, and then collapsing all the states that depend on that qubit, and then re-normalizing. I also had the Qubits reversed in my diagram which led to some very confusing bugs.

Conclusion

Anyways just some fun stuff I’ve been up to. Being 100% honest, I’m not always the best at responding (sorry), but if you have any questions or comments feel free to reach out! c0nrad@c0nrad.io

I’m hoping I’ll have the Quantum Hash Cracking algorithm out soon. But in the meantime I still need to learn some other stuff first, so probably a few more algorithms first.