Calculating scattering angles from fully elastic spherical collision.

Background

In one of my first blog posts, I talked about the difficulty I had with calculating the resulting angles from a collision of two spheres.

I could bounce objects off each other, but not at an angle.

Well, fast forward to today (5 months later), I’m now in school for physics (undergrad)! And a little bit better prepared to tackle the problem.

I reached out to my professor of classical mechanics about the above problem, and he suggested I read Ch. 14 of Taylor’s Mechanics on Collision Theory. The chapter was pretty interesting, and it was stuff I wanted to learn sooner or later. I’m hoping soon I can start modeling particle collisions (a long term goal of mine, I’m about halfway through “Elementary Particles” by Griffiths).

Anyways, in Taylor’s book, example 14.5 talks about hard sphere scattering, and it turns out that the angle of incidence and reflection are equal. Kind of reminds me of bouncing photons off a medium.

To be honest, I don’t quite understand why the angles should be equal. There’s probably some beautiful action/Lagrangian minimization that shows that it must be the path. I’ll solve that another day.

But, poking around some more, I found out that wikipedia lists the equations I needed:

$$ \bm{v_1 \prime} = \bm{v_1} - \frac{2m_2}{m_1 + m_2} \frac{ < \bm{v_1} - \bm{v_2}, \bm{x_1} - \bm{x_2}>}{ || \bm{x_1} - \bm{x_2} ||^2} ( \bm{x_1} - \bm{x_2}) $$

$$ \bm{v_2 \prime} = \bm{v_1} - \frac{2m_1}{m_1 + m_2} \frac{ < \bm{v_2} - \bm{v_1}, \bm{x_2} - \bm{x_1}>}{ || \bm{x_2} - \bm{x_1} ||^2} ( \bm{x_2} - \bm{x_1}) $$

With this, I could put a bunch of balls into a container and watch them bounce! I think I might use this in the future to do some Statistical Mechanics/Boltzman entropy modeling fun later:

Scattering

Anyways, I figured it’d be fun to build something similar to Rutherford’s Scattering Experiment:

(Code)

It turned out pretty nice.

From this I was able to plot the scattering angle against the impact parameter (b, how much offset the two items are).

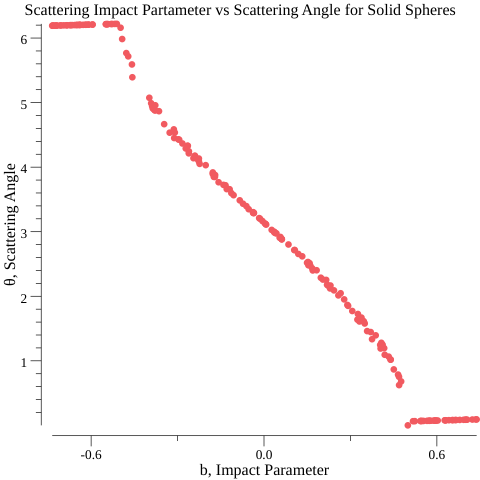(Code)

Pretty neat stuff. It’s cool how often stuff bounces back. I imagine this is probably similar to what Rutherford saw all those years ago.

What was difficult

• In terminal, character height is twice as much as character width, so the points appears to move much faster in one direction. So instead the renderer now treats one character height as 2 units of length
• I’m using a very simple time-stepping integrator, and some of the incident angles are pretty sensitive, so if the ball moves to fast I’ll get nonsense collision angles since the circles will be on top of each other
  • The correct thing to do would be to reverse the simulation till the two spheres are at the point of collision, and then calculate the angles
  • Being lazy, I just set the timestep to 1000 frames/second, in the future I’ll go back and do it correct

Otherwise not much. I wish I understood the math behind the collisions better.

What went well

• I really prefer doing graphics in terminal compared to rendering in 3d with webgl, being able to quickly iterate is very nice.

Future

Probably nothing for this project. Up next I want to calculate the Clebsh-Gordan coefficients. Eventually I’ll come back to this for elementary particle collisions. First will probably be relativistic collisions.