Shor’s algorithm is probably the most well known quantum algorithm. But it turns out I didn’t understand it as well as I thought.
Introduction
I’m somewhat giving up on this problem. I got a working version, but I’m not happy with it.
Spoiler, I thought the hard part of Shor’s algorithm would be the Quantum Fourier Transform. It turns out the hard problem is multiplying two numbers!
Anyways, this post will give a super introductory look into RSA, Shor’s algorithm, and some rants about multiplication.
Shor’s
This was the first Quantum Algorithm I heard about (my background is computer security). Using Shor’s algorithm you can factor large numbers. Which at the surface seems pretty unexciting, but then we remember that a lot of the world’s security is based on the fact that it’s hard to factor numbers. Factoring numbers is of huge importance.
RSA
RSA (and other asymmetric algorithms) are pretty cool. It’s a way to securely communicate with someone you’ve never met before, while others are listening. To prove to yourself how cool it is, try this thought experiment:
Lets say you found yourself in jail, and you knew a terrible secret, and you wanted to notify a news agency of the terrible secret. But the guards are reading your letters. You’ve never met the news agency before. Can you hide a message in letters that only the news agency would find?
Or a more real example, imagine you’re sitting at home, ordering something online from amazon.com, you need to give amazon.com your credit card, but there’s probably 10-20 computers/routers in between you and the amazon.com servers that will be reading every message you send as it goes to amazon. Can you securely send your credit card?
The following ideas will not work, because the guard/servers will know what to look for:
- “Hey amazon, look at the first letter of every sentence”
- “Hey amazon, use the following encryption algorithm with this key: abc123”
With no prior knowledge it’s pretty difficult (but not impossible). This is why RSA (and other asymmetric algorithms) are pretty cool.
Instead you rely on the fact that it’s hard to factor prime numbers (and some number theory), it’s possible.
RSA Algorithm
(This is a purposely wrong/simplified algorithm, it only carry’s the spirit of RSA for simplicity.)
-
If I want to send amazon a message I can take two large prime numbers and multiply them together N = p*q. Using the original p and q I can do some number theory to generate a D, and E, which are two other numbers that have special inverse properties. I then throw away p and q. Since no one can determine what p and q are, my algorithm (specifically my D number) is safe.
-
Then I send amazon/friend my E number (along with N). E is the public key. Since it’s a public key it can be sent/seen by anyone, (including the attackers)
-
Amazon/friend can then take a private message they want to send me and perform the following math:
$$ ciphertext = message^E mod N $$
And send me the ciphertext.
- The only way to decrypt the ciphertext and get back the message is if you have the other number (D).
$$ message = ciphertext^D mod N $$
I now have the private message they sent me. They either sent their public key, or if they were smart they would have sent a “symmetric private key” that we could use with another symmetric cryptographic algorithm such as AES. (RSA is very computationally expensive. Much easier to use AES if you can)
At this point we have sent a secure message and can easily send more secure messages. And the guards can intercept every message, and have no idea what is going on.
Breaking RSA
But, using shor’s algorithm you can figure out the factors of N. The D/E numbers are based off the original p and q numbers (N = p*q). Using the D number you can decrypt any message.
So, if the guard/server had a quantum computer that ran shor’s algorithm, they could decode all the messages by factoring N and computing the D number.
Shor’s Algorithm
Shor’s algorithm is pretty nifty too. The quantum computer doesn’t just factor the numbers, you have to reframe the problem. That’s the genius behind shor’s algorithm.
Instead you convert the problem such that it has a cyclic answer. Then you take the Quantum Fourier Transform, do some more math, and the factors pop out.
The “math” that the quantum algorithm solves is \( a^{x} mod N \), where N is the prime number, a is some random number, and “x” is the number in super position. We have to find the period of this function. (How long until the function repeats itself).
Normally to find the period you have to check the function over and over until it repeats. Classically this could take a very very very long time, but with a quantum computer we can try all the inputs at once, and then extract the pattern (thanks to QFT).
Once you find the period of the function, you simply take the GCD of two numbers to get the factors:
$$ f1 = GCD(N, a^{period/2} + 1) $$ $$ f2 = GCD(N, a^{period/2} - 1) $$
These equations are based on Euler’s Theorem. f1 and f2 are our two factors. (So for 15, 3 and 5).
Why Multiplication Is Hard
I did not expect this. But it turns out the hard part of this was the multiplication!
Multiplication requires a bunch of intermediate steps, and this quickly explodes the number of qubits you need to do computation. In the classical circuit you can destroy intermediate results and re-use them. But not so much in the quantum computer, every step must be reversable if you want it to be a real quantum gate. Multiplying a 3bit number by 3 bit number quickly went to more than 10 qubits, and then I gave up. (It’s probably horribly inefficient, but I couldn’t find any simple solutions).
My quantum computer is horribly inefficient overall too, and even at 10qubits it’s very very slow. (if I optimized/cached some of the matrix code, I could speed it up to probably 16 qubits). But, it’s just disappointing to be thwarted by something so simple. I have a new appreciate for multiplication.
Slightly cheating
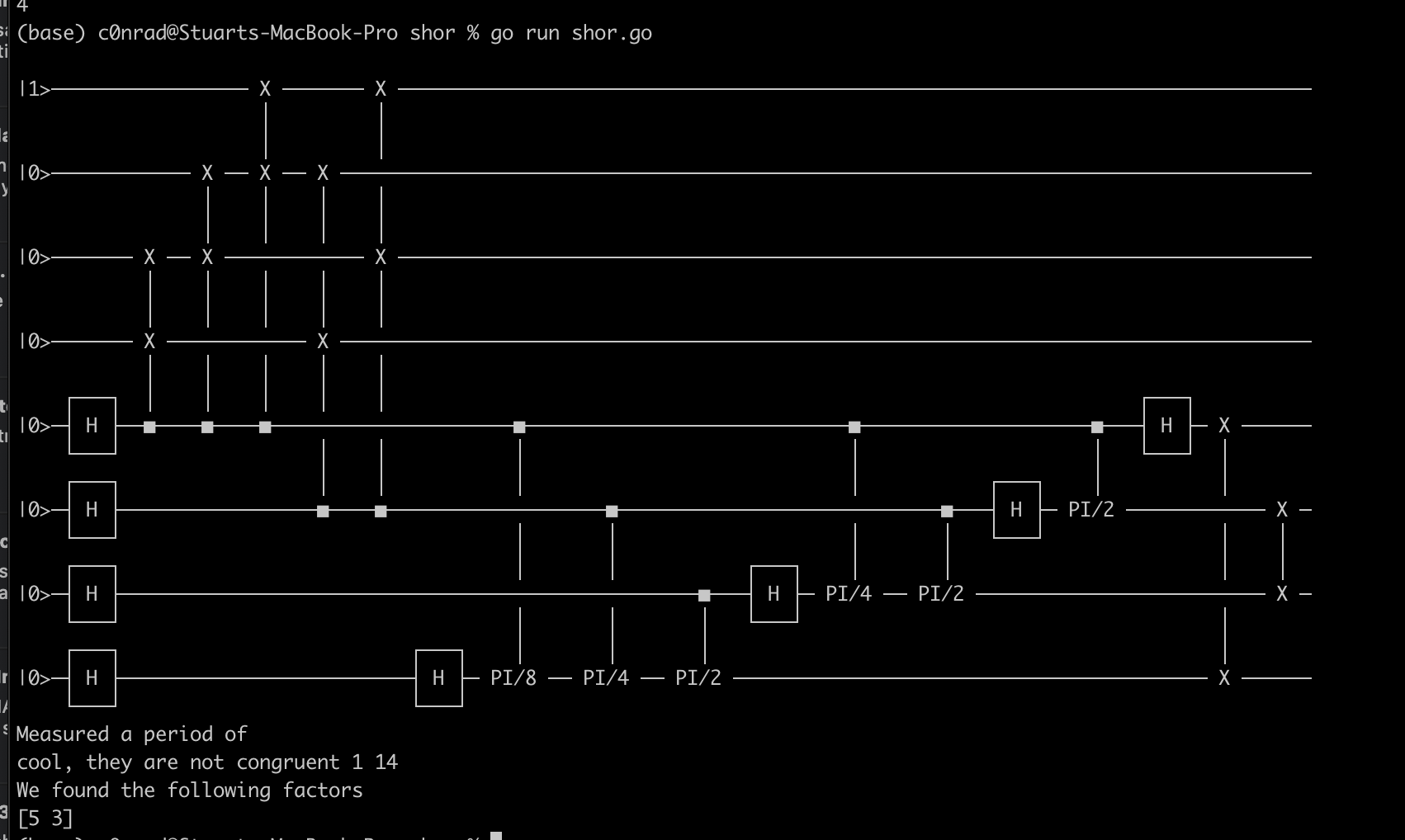
So, instead the shor’s algorithm implemented above is just something I copied from Programming Quantum Computers Essential Algorithms. It only works for 15 with a co-prime of 2.
One day I’d like to revisit this, but I need to take a break.
Factor Via Grovers
I also thought I would be sneaky and just factor the number’s using Grover’s algorithm, but again it’s taken me longer than I would like to build a non-wasteful circuit that does multiplication.
But it seems reasonable that if there was an efficient multiplication, I could just create a quantum circuit with two registers A and B, and my oracle function would be return A*B == N. Then it would only require PI * Sqrt(N)/4 iterations.
Conclusion
Overall the last few days were frustrating. But progress was made. I’m super happy that my little quantum computer can even solve a specific case of shor’s, but disappointed I couldn’t go further at this time.
I’ll be taking a quick break from Quantum Computing to learn more of the basics. I just picked up a book on numerical methods, I think I’ll have some fun with that.