Introduction

The Ising model is a pretty nifty little model. From just some simple nearest neighbor interactions and binary spin states, we can get non-trivial behavior. I attempted to solve for the critical temperature, but it will be that non-trivial behavior that will be the reason I was unable to solve for the critical temperature.

Critical Temperature

One thing that is neat about the Ising model is that when the temperature drops below the “critical temperature”, the model will break symmetry and randomly magnetize in one direction.

The calculation of that critical temperature has been done for the 2D Ising Model \( \frac{2}{\ln{(1 + \sqrt{2})}} \), but not the 3D model. There was some recent research in the area, but as far as I know, no exact solution.

What a fun challenge to attempt!

My failed attempt

The big picture of my attempt: For a specific magnetization and temperature, why not calculate the probability that we move towards “conforming magnetization” or away from it. We do this by counting states and then multiplying a lot of probabilities together (basically following a single step of the metropolis algorithm, multiple steps if nothing happens).

I started with the 2D model since this method should easily extend to 3D, and we can verify it works in 2D.

The code can be found here.

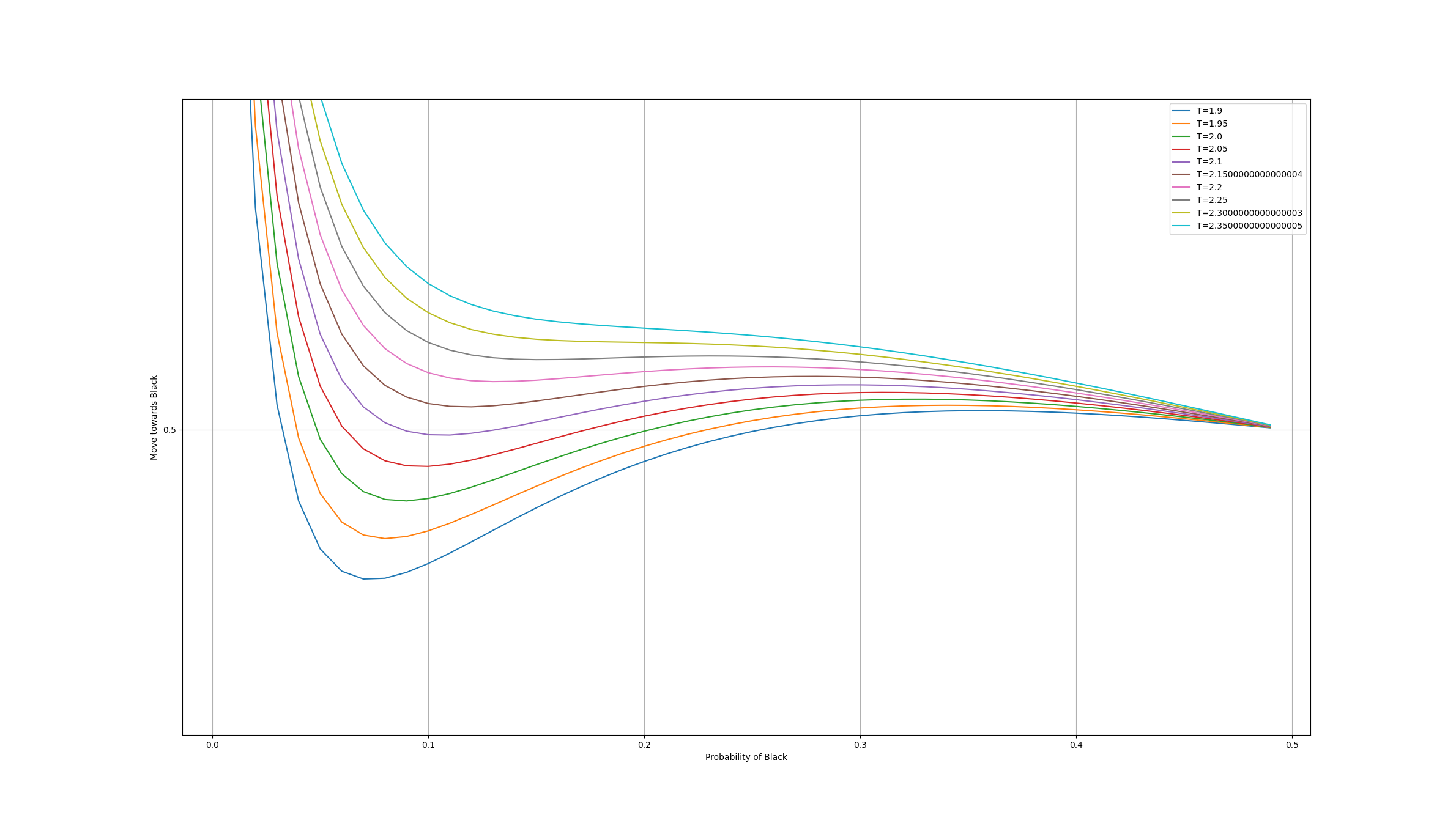
It produces images like this:

We can see that for different temperatures, the simulation will tend towards “conforming magnetization” or away to randomness.

I already knew it didn’t seem right, but I plugged it into sympy and took some derivatives and plots of this 2D function:

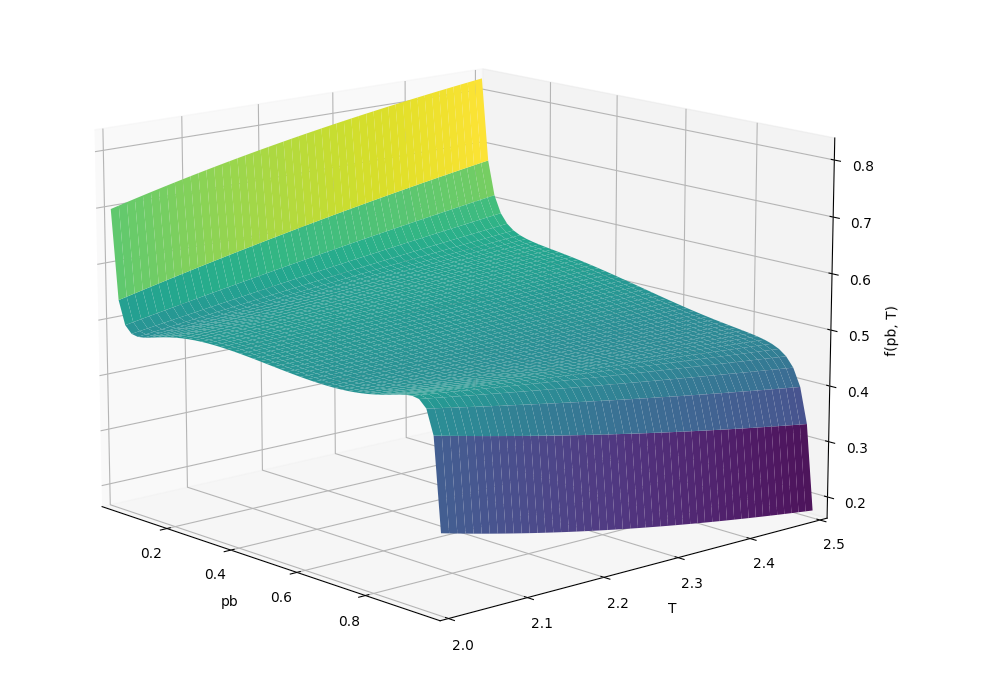
The exact critical temperature we’re looking for is around 2.269. And we’re looking for the temperature that just kisses the X axis, which on the plot is around 2.1.

What went wrong

For this algorithm to work, I calculate the probability of each local spot occurring (example: a spin up in the middle, with 3 spin down neighbors). Since we’re looking at 5 different spots at once (middle, plus 4 neighbors), there’s 2^5 (32) different types of spots. So we just calculate the probability that each state will switch or not towards chaos (using metropolisis), and multiply it by the probability of that specific spot occurring.

To calculate the probability of a spot occurring, I use the overall magnetization \( M \) and just make a naive \( M^4 \) sort of calculation to get the probability that all the neighbors are spin up (and continue for the other 31 states).

This would work fine if there wasn’t non-trivial behavior.

The problem is that Ising is non-trivial! There are domains of similar spins, so I can’t just say the probability of all spin ups is \( M^4 \), it’s slightly more likely since they like to group up compared to just have one spot of off color.

.

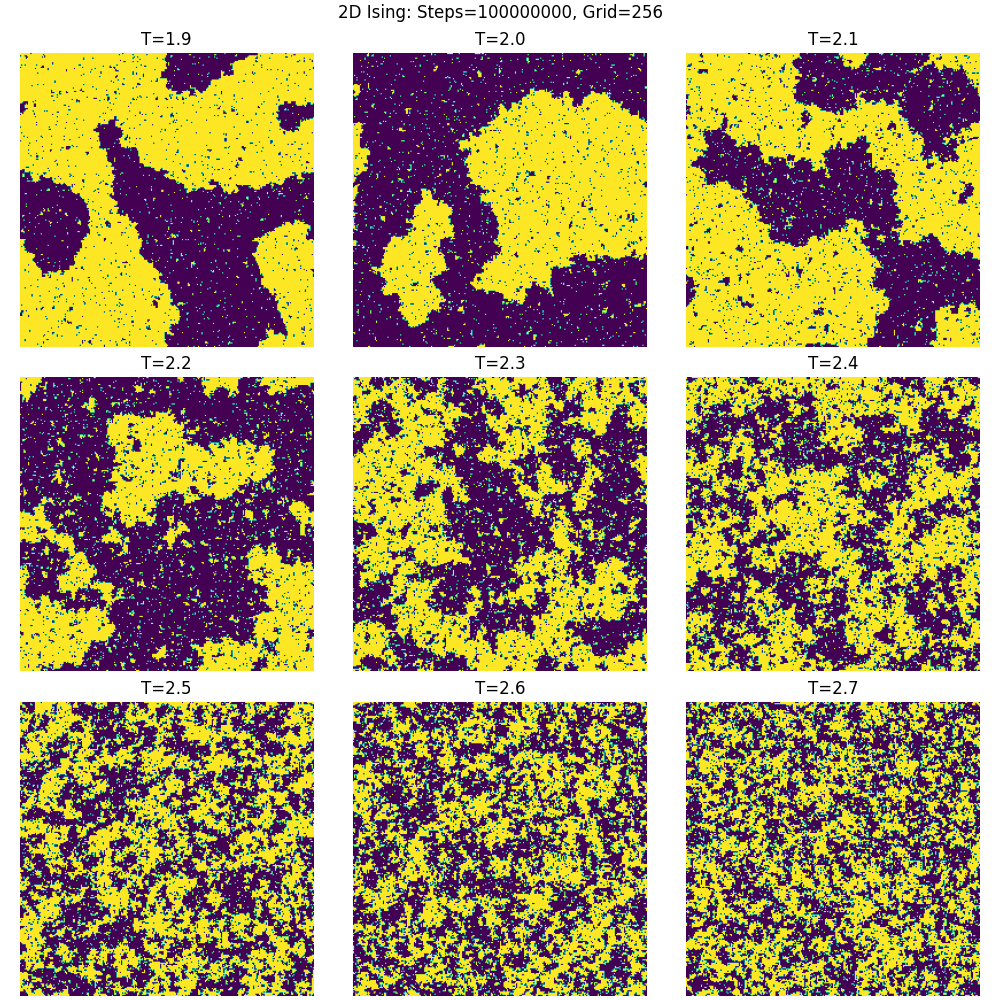You can see above that even with an equal probability of purple or yellow at the critical temperature, it’s not evenly spread around, it’s clumpy.

A bandaid attempt

Okay, so we can’t use the average magnetization to calculate the probability of each of the 32 local states. Can we use nearest neighbor spin correlation functions \( <s> \)?

I again naively thought we could just find some \( s(M, T) \) (what is the probability that a neighbor is the same color given a magnetization and temperature) function that would give us the correct number, (spoiler that also won’t work, for reasons later).

So, I tried to fit a function to \( s(M, T) \) (data taken from long running simulations):

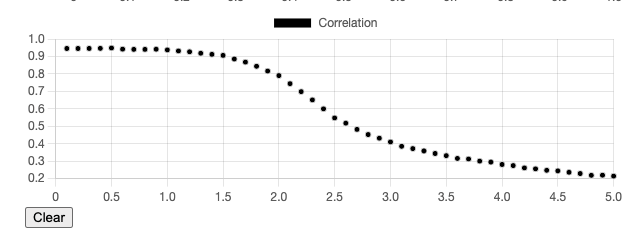
But I was unable to find a function that fit exactly. (I was reading an older book that says it hasn’t been solved for the 2D case, which makes sense)

And recently I realized this idea was also flawed from the start. For example, there are two different states that have three white cells (with one in the middle). You could have the three white cells in a line, or the three white cells in the corner. Both would be the same probability according to \( s(M,T) \) but due to the non-trivial grouping, they should not have the same probability.

Conclusion

I was a little disappointed that the method didn’t end up working out. It was an exciting few days getting everything working, and finding the flaw was a little but heartbreaking, but I ended up learning a lot. And my calculations were surprisingly close to the exact solution!

Not sure what is next, maybe I’ll finally do the QFT electron magnetic moment calculation.