It’s been awhile since I’ve posted, so I figured I’d talk about what I’ve been working on for the last few months. Specifically some new attempts for solving the Ising models.

Puzzle Piece Representation of the Ising model

The “puzzle piece” representation of the ising model is my attempt to find a simpler solution for 2D (and hopefully one that extends to 3D).

To be honest, it’s not that well motivated. I just have a gut feeling that it seems interesting. This blog covers the results so far.

In the puzzle piece representation of the Ising model, we no longer look at individual spins, but instead groupings of spins. For the 1D ising model, this is groups of three spins (middle, and the one to the left and right). For 2D ising model, this is groups of 5 spins (middle, up, right, down, left).

Why? Again, it’s not well motivated, but a single spin by itself doesn’t mean anything. All the useful information of the Ising model is the relationship between a spin’s neighbors. So with three spins together, we know what the spin looks like on both sides.

Puzzle Piece State Vector

So instead of characterizing the state of an Ising model by a bunch of spin ups and spin downs, we instead can specify it by the density of the above states.

As an example, if we had a chain of 100 spins that were all spin up, we’d say the state is \( |a=1 \rangle \). If one of the spins was spin down, we’d instead have \( |a=.99, c=.01 \rangle \).

One neat thing about representation is we can now specify infinite length Ising models. The state vector tells us the probability that a specific spin is of a specific type.

There’s a lot of ising states that collapse to the same Ising vector. In the above example with \( |a=.99, c=.01 \rangle \), there are 100 states that collapse to the same ising vector. (This is because of the translational invariance, the single down state can be anywhere.) This collapse is both a blessing and a curse as we will see later.

What can we say with this new representation?

Total Probability

We know that the probability of all the states must add up to one.

$$ a + b + c + d + e + f = 1 $$

Energy

We can also easily calculate the energy (per spin) of the model:

$$ U/N = a - c + d - f $$

Magnetism

The magnetism can be calculated by just looking at the center of each state:

$$m/N = a + b + c - d - e - f $$

Detailed Balance

Since we are going to deal with equilibrium states, we can also use the principle of detailed balance.

$$ p(a) p(a \rightarrow f) = p(f) p(f \rightarrow a) $$

If we use metropolis acceptance conditions, we get the following:

$$ a * e^{-2/t} = f $$ $$ b = e $$ $$c = d* e^{-2/t}$$

Expectation Value Symmetry

We also know that there’s no preference for spin up or down if we look at many systems, so we can say that the expectation value for the spin-up-centered states must equal the spin-down-centered states.

$$ \langle a(t) \rangle = \langle d(t) \rangle $$ $$ \langle c(t) \rangle = \langle f(t) \rangle $$

r=1 and r=2 correlation

We can calculate the r=1 and r=2 correlations between spins by just adding up

What do the states look like?

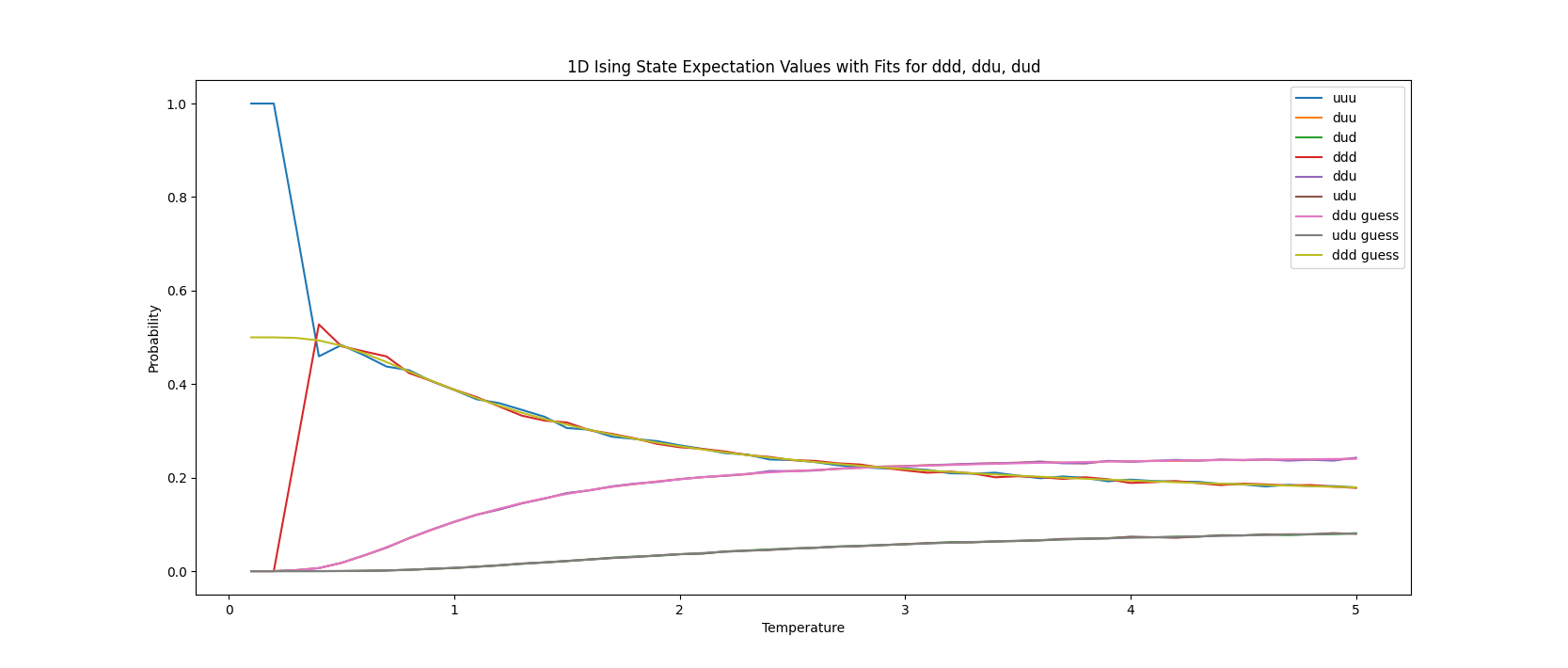
(Kind of a spoiler from the plot, I was able to determine the expectation values for each of the state as a function of temperature.)

But we can see that either the all up or all down states will dominate at low temperatures, and at high temperatures the states will be equal their random sampling probability.

State Solutions

Since the 1D ising model was already solved, I was able to work backwards and figure out what the states must be.

$$ \langle a(t) \rangle = \frac{1}{8}(1+\tanh(1/t))^2 $$ $$ \langle b(t) \rangle = \frac{1}{4}(1-\tanh(1/t)^2) $$ $$ \langle c(t) \rangle = \frac{1}{2 ( 1 + e^{2/t})^2} $$

To do this I used the known correlation length of the 1D ising model \( tanh(1/t)^r \), and then calculated the r=1 correlation and r=2 correlation from the states and put them into mathematic to solve (\( a - c = \tanh(1/t),a - b + c + d - e + f == \tanh(1/t)^2 \)).

Calculating Specific Heat

We can calculate the specific heat by taking the derivative of the energy with respect to temperature. If we do this, we get the correct specific heat:

us[t_] := -2*as[t] + 2*cs[t]
D[us[t], t] // FullSimplify
-> Sech[1/t]^2/t^2

What’s next

• We had to cheat to get the state equations, is it possible to find them without using the known solution?
• Can we use the solution to calculate the multiplicity of states that would allow us to go back and forth between the standard ising model and this new state vector?
• Is it possible to calculate the entropy using this new state vector that agrees with the known result?