Some exploration into numerical differentiation.
Introduction
I just picked up a new book: Basic Concepts in Computational Physics. I’ve been planning on building simulators for EM and Relativity. But after doing some research on how other people built them, I realized I should probably learn some of the basics of computational physics first. Other people seem to use FDTD (Finite-Difference Time-Domain) for simulations, and I have no idea what that is.
To the drawing learning board!
The first chapter was on Numerical Differentiation. Here’s some fancy charts and explanations I made after implementing the chapter in code.
Differentiation
Differentiation is about finding the slope of some function. In middle/high school we learned that we could find the slope of a linear line by:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
But not all functions are that easy to differentiate. And sometimes you’re lazy and don’t want to figure it out. Or sometimes you only have some data and not the underlying function. Turns out you can use computers to get pretty good estimations!
Forward, Backward, Center Numerical Differentiation
In high school calculus we learned that:
$$ f^\prime(x) = \lim_{h\to\infty} \frac{f(x+h) - f(x)}{h} $$
And the idea behind numerical differentiation isn’t that different. But instead of taking the limit, we just make h very small. When h is very small, we just assume the line is linear and use the equation for finding the slope of a linear line.
But, we need to make a choice. Let’s say we want to find the slope at \( xi \) should we use \( x{i-1}, x*{i} \) as the two points? Or \( x*{i}, x*{i+1} \) or maybe \( x*{i-1}, x_{i+1} \)?
$$ f^\prime*{forward}(x_i) = \frac{ f(x*{i+1}) - f(xi) }{h} $$ $$ f^\prime{backward}(xi) = \frac{ f(x{x}) - f(x*{i-1}) }{h} $$ $$ f^\prime*{center}(xi) = \frac{ f(x{i+1}) - f(x_{i-1}) }{2h} $$
It turns out the answer is the last one (called Center), but we can go one step further and prove that using the point before and after is the best using Taylor series!
Determining the error using Forward, Backward, Center Numerical Differentiation
We can actually prove that the center method has the least amount of error.
Let’s Taylor expand \( x*{i-1} \) and \(x*{i+1} \). So we’re using f(xi) as our base point and estimating \( x{i-1} \) and \(x_{i+1} \).
$$ f(x*{i-1}) = f(x*{i}) - h f^\prime(xi) + \frac{h^2}{2}f^{\prime\prime}(x_i) - \frac{h^3}{6}f^{\prime\prime\prime}(x_i) + … $$ $$ f(x{i+1}) = f(x_{i}) + h f^\prime(x_i) + \frac{h^2}{2}f^{\prime\prime}(x_i) + \frac{h^3}{6}f^{\prime\prime\prime}(x_i) + … $$
With
$$ h = x*{i+1} - x_i = x_i - x*{x-1} $$
Now we can re-arrange some stuff from the \( f(x_{x-1}) \) equation to determine the error for the Forward Differentiation method:
$$ \begin{array}{llll} f^\prime_{forward}(x_i) & = \frac{ f(x_{i+1}) - f(x_i) }{h} \\ & = \frac{ (f(x_{i}) + h f^\prime(x_i) + \frac{h^2}{2}f^{\prime\prime}(x_i) + \frac{h^3}{6}f^{\prime\prime\prime}(x_i) + …) - f(x_i)}{h} \\ & = f^\prime(x_i) + \frac{h}{2}f^{\prime\prime}(x_i) + \frac{h^2}{6}f^{\prime\prime\prime}(x_i) + … \\ & \sim f^\prime(x_i) + \mathcal{O}(h) \end{array} $$
Doing the same for Center we get:
$$ \begin{array}{llll} f^\prime_{center}(x_i) & = \frac{ f(x_{i+1}) - f(x_{i-1}) }{2h} \\ & = \frac{ (f(x_{i}) + h f^\prime(x_i) + \frac{h^2}{2}f^{\prime\prime}(x_i) + \frac{h^3}{6}f^{\prime\prime\prime}(x_i) + …) - (f(x_{i}) - h f^\prime(x_i) + \frac{h^2}{2}f^{\prime\prime}(x_i) - \frac{h^3}{6}f^{\prime\prime\prime}(x_i) + …) }{2h} \\ & = f^\prime(x_i) - \frac{h^2}{6}f^{\prime\prime\prime}(x_i) + … \\ & \sim f^\prime(x_i) + \mathcal{O}(h^2) \end{array} $$
| Forward Difference | $$ f^\prime_{forward}(x_i) = \frac{ f(x_{i+1}) - f(x_i) }{h} $$ | $$ \mathcal{O}(h) $$ |
| Backward Difference | $$ f^\prime_{backward}(x_i) = \frac{ f(x_{x}) - f(x_{i-1}) }{h} $$ | $$ \mathcal{O}(h) $$ |
| Center Difference | $$ f^\prime_{center}(x_i) = \frac{ f(x_{i+1}) - f(x_{i-1}) }{2h} $$ | $$ \mathcal{O}(h^2) $$ |
The error can be a little confusing to understand, but it’s saying that if we want 100x better resolution on forward or backward methods, we’d need to split our \( h \) into 100x smaller buckets.
Whereas for the center method, if we want a 100x improvement, we only need to split our \( h \) buckets by 10. 10*10 = 100.
Let’s see this in practice!
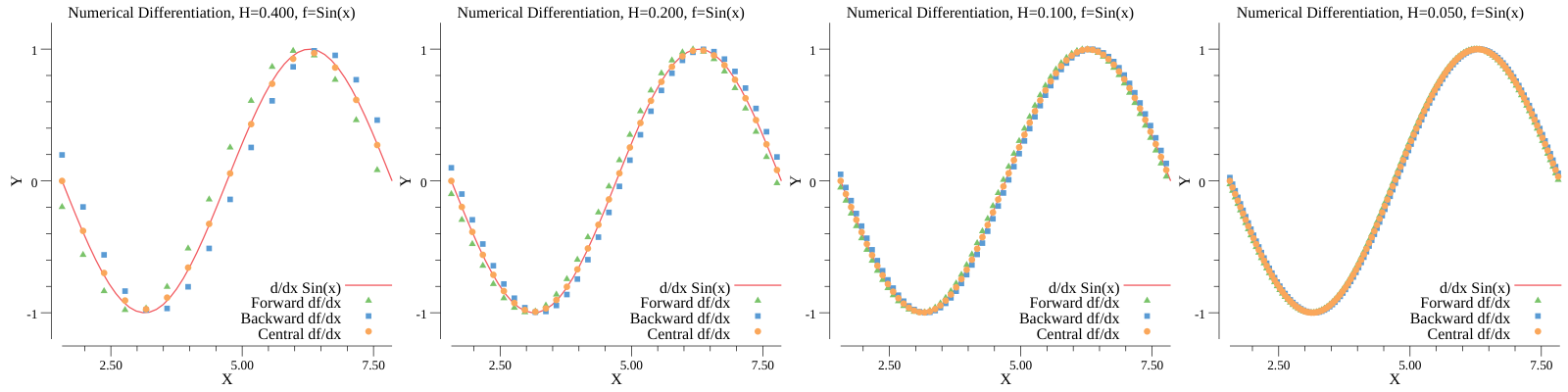
Forward Backward Center using different H sizes
Here I take the derivative of \( sin(x) \) using the forward, backward and center methods using different buckets of h. You can see that the Center method is significantly better.
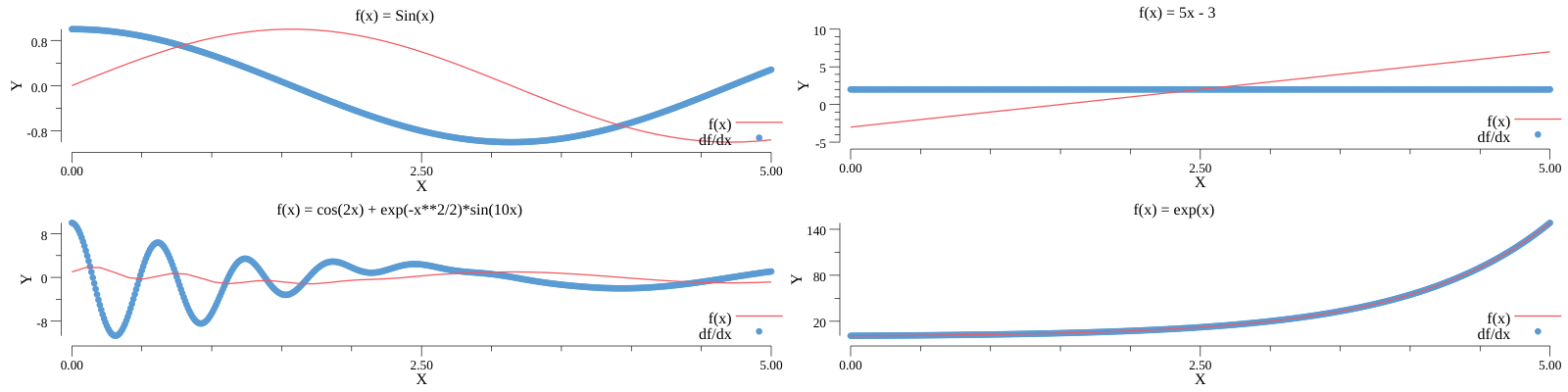
Random Derivative Examples
The numeric differentiator is just plain cool how simple it is!
Here I use Numerical Differentiation to plot the derivatives of the following equations:
$$ f_1(x) = sin(x) $$ $$ f_2(x) = 5x -3 $$ $$ f_3(x) = e^x $$ $$ f_4(x) = cos(2x) + e^{-\frac{x^2}{2}} sin(10x) $$
Legendre Polynomials
In my electron orbitals simulator I had to calculate the Legendre Polynomials (using Rodrigues’ Formula):
$$ P_l(x) = \frac{1}{2^l l!} \left(\frac{d}{dx}\right)^l (x^2 - 1)^l $$
Knowing that I’d have to calculate the derivative of this function was one of the reasons I decided to check out GiNaCs in the first place. (GiNaCs has a symbolic differentiator).
But now with a Numeric Differentiator, I have no need for the symbolic executioner! (Obviously not fully true, it’s still extremely nice to have the symbols).
But, damn, it is so satisfying generating the polynomials like this in Go. I’m in shock that it even works to be honest. I heavily abuse function closure’s to store state. (It’s function closure’s all the way down):
func LegendrePoly(l int) Func {
prefix := 1 / (math.Pow(2, float64(l)) * Factorial(l))
inner := func(x float64) float64 {
out := 1.0
for i := 0; i < l; i++ {
out *= x*x - 1
}
return out
}
out := inner
for i := 0; i < l; i++ {
out = D(out)
}
return func(x float64) float64 {
return prefix * out(x)
}
}
But with some plotting, we can verify it works!
How cool is that!
Conclusion
Numeric differentiation ended up being way cooler than I thought it would be.
Up next is numeric integration! I had to build a numeric integrator for a previous game engine, I’m excited to see how wrong I was.