Solving Laplace’s/Poisson’s equation using the method of relaxation.

Overview

This post covers a little tool I built for solving Laplace’s/Poisson’s equation using Method of Relaxation.

It starts with some background on solving electrostatics problems, different solution types, and then the “Method of Relaxation”. This can be used to determine the electric/potential field in some region of space given appropriate boundary conditions.

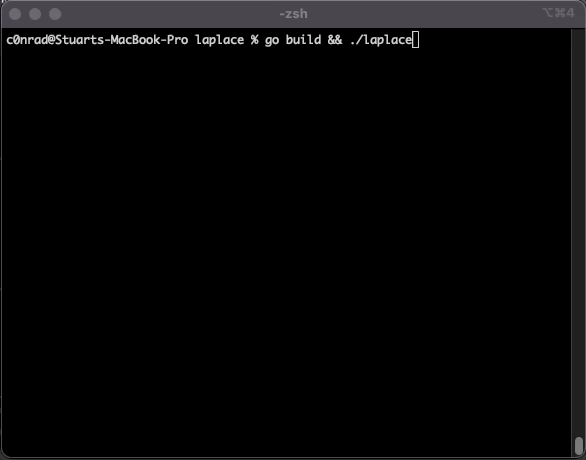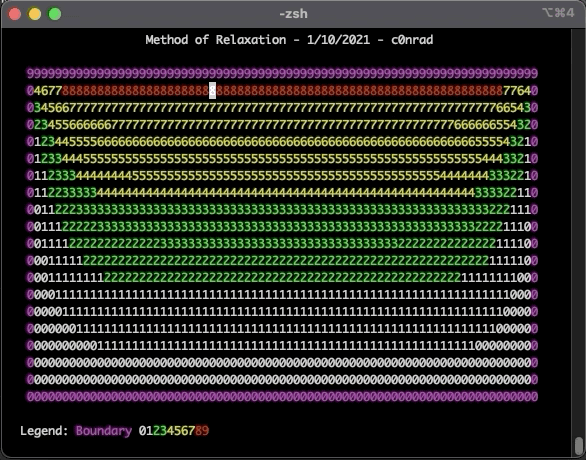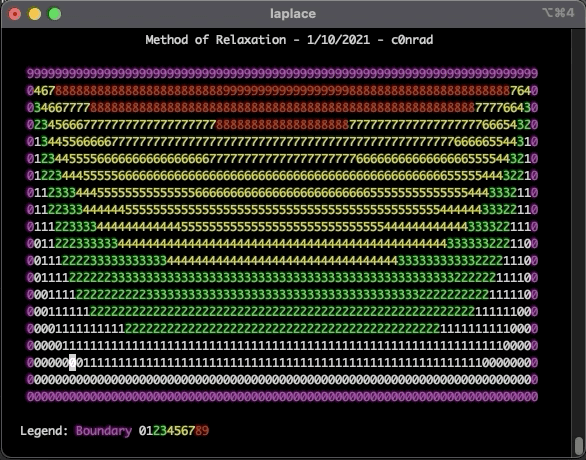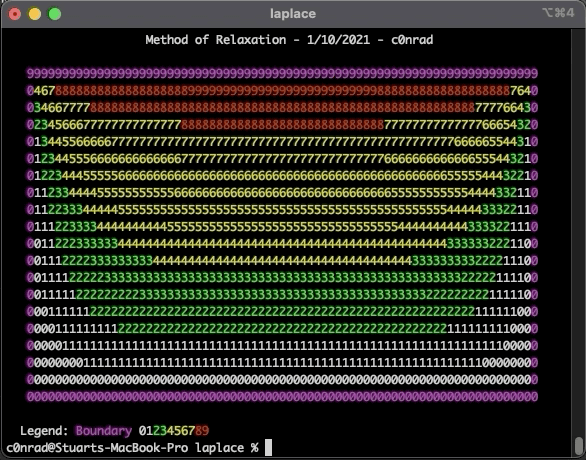
The tool that was built is not useful for anything, just for learning purposes.

Background

The Problem

Most electrostatic problems involve finding the electric field given a static charge distribution. The charge distribution can be a set of point charges \( q \), a line charge \( \lambda \), a surface charge \( \sigma \), or a charge density \( \rho \).

The relation between charges and electric field is given by Coulomb’s law:

$$ \bm{E}(\bm{r}) = \frac{1}{4 \pi \epsilon_0 } \int \frac {\hat{\bm{r}}}{r^2} \rho(\rm{r\prime})d\bm{r}\prime $$

But in situations where there isn’t a symmetry we can (ab)use the integral can get pretty nasty.

Instead we can tackle the problem of determining the electric field by using Poisson’s equation:

$$ \nabla^2 V = -\frac{1}{\epsilon_0} \rho $$

Poisson’s equation comes from combining Gauss’s law (in differential form) \( \nabla \cdot \bm{E} = \frac{\rho}{\epsilon_0} \) and the definition of electric potential \( E = -\nabla V \). Gauss’s law simply states that the divergence (the amount of “stuff” flowing out) must be equal to the amount of charge inside that’s generating the flow. It sounds obvious, but having it in mathematical form is extremely useful.

Poisson’s equation says that if we take the Laplacian ( \( \nabla^2 V = \frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} + \frac{\partial^2 V}{\partial z^2} \)) of the electric potential we will get the charge density. Once we know the potential we can easily convert to the electric field.

Commonly we want to calculate the electric field where there is no charge density. There is charge nearby, but not in the region of space we are interested in evaluating. In this case Poisson’s equation becomes Laplace’s equation:

$$ \nabla^2 V = 0 $$

This is the specific equation we are interested in solving.

So an example problem would be: imagine we have a box of conductors with one side having a specific charge (or is being held to a potential), and the rest of the sides are grounded (held to a different potential), determine the potential/electric field.

Laplace’s equation

The solution to Partial Differential Equations (PDEs) such as Laplace’s equation can be tricky to solve. The solutions can contain an arbitrary number of constants. (There’s not a general solution.)

But there are certain properties that solution of Laplace’s equation will contain that will be useful.

The most important property that we will use is the fact that solutions of Laplace’s equation are “boring”. They are actually the most “boring” they can be. The solution curves are smooth, and any point in the solution is the average of all nearby points.

Boundary Values

To actually solve for the potential, we also need the boundary values of the space we are interested in. The two boundaries we can use are either:

1. Dirichlet Boundary Condition: The potential along the surface of the volume
2. Neumann Boundary Condition: The normal derivative of the potential along the surface

There’s also something called the “uniqueness theorem” which states that if we can find one solution that fits laplace’s equation and the boundary values, we actually found the only solution to the problem. This is extremely profound. There’s a couple of technicalities, but they are minor (such as technically it’s the electric field that is unique).

Solutions

Method of relaxation

“Method of relaxation” is the numeric approximate solution to determining V given the boundary conditions.

In two dimensions this is the equation we are trying to solve:

$$ \frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} = 0 $$

If we split our experiment into a set of grid points, and then use the official definition of a derivative (the limit definition) twice, we can get an estimation for the second derivative:

$$ \frac{\partial^2 V}{\partial x^2} = \frac{V(x+a, y) + V(x-a, y) - 2 V(x, y)}{a^2} $$

Then combining both the x and y direction, and doing some re-arranging we can get an equation for the value of each grid point:

$$ V(x, y) = \frac{1}{4}[ V(x+a, y) + V(x-a, y) + V(x, y+a) + V(x, y-a)] $$

This says that roughly each point can be thought of as the midpoint between the four points next to it.

Solution

So we’ll setup a grid, give it some boundary values that never change, then iterate over the grid with the above equation until we’re happy with the results.

The code can be found here:

https://github.com/c0nrad/relaxation

Separation of Variables

We won’t be analyzing these here, but using separation of variables we can get an analytical solution. In separation of variables we assume the solution is actually a combination of two/three functions multiplied together that each only depend on one variable. It’s a big simplification, but it actually works and a solution can be plucked out. Separation of variables is used in a lot of different fields of physics. (For example, separation of variables was used for the hydrogen model).

Using separation of variables in spherical coordinates for solving laplace’s equation we get out some harmonic functions which is pretty neat!

You can also solve them using Green’s functions (which are integrals on dirac delta functions). I’ll talk about these at some point in the future.

Conclusion

It was a fun afternoon project. But I don’t think I’ll be extending it at all.

Up next I think I’ll try to simulate different types of Ion Traps using emmy.