Plot the effective potential for the two body force simulation.
Overview
We can further simplify the equation of motion for the two-body-central-force problem, and also derive a quantity called the “effective potential”.
We will then update our simulation to plot this effective potential.
Polar Coordinates
In the last simulation, we were able to reduce our two body problem to the following Lagrangian:
$$ L = \frac{1}{2} (M \bm{\dot{R}}^2 + \mu \bm{\dot{r}}^2) - U(r) $$
We then chose our frame of reference such that \( \bm{R} = 0\) and \( \bm{\dot{R}} = 0\).
So we are left with:
$$ L = \frac{1}{2} (\mu \bm{\dot{r}}^2) - U(r) $$
Currently \( \bm{r} \) is a cartesian coordinate, but we can convert it to polar coordinates. \( \bm{\dot{r}} = \dot{r}\bm{\hat{r}} + r \dot{\phi}\bm{\hat{\phi}} \). It’s a little confusing keeping all the terms straight. But remember that \( \bm{r} \) is a vector of (x,y,z), and \( r \) is a scalar quantity of length. \( \bm{\hat{r}} \) is a unit vector pointing in the direction of \( \bm{r} \).
$$ \bm{\dot{r}}^2 = \dot{r}^2\bm{\hat{r}}^2 + r^2 \dot{\phi}^2\bm{\hat{\phi}}^2 + 2\dot{r}\bm{\hat{r}} r \dot{\phi}\bm{\hat{\phi}} $$
But \( \bm{\hat{r}}^2 = \bm{\hat{\phi}}^2 = 1 \), and \( \bm{\hat{r}} \bm{\hat{\phi}} = 0 \), therefore:
$$ \bm{\dot{r}}^2 = \dot{r}^2 + r^2 \dot{\phi}^2 $$
So our new Lagrangian is:
$$ L = \frac{1}{2} \mu (\dot{r}^2 + r^2 \dot{\phi}^2 ) - U(r) $$
Solving Lagrangians
Now we have two coordinates to solve for: \( r \) and \( \phi \). (This r is different than before, this is a scalar r as opposed to our relative vector \( \bm{r} \)).
$$ \frac{d}{dt} \frac{\partial L}{\partial \dot{\phi}} = \frac{ \partial L}{\partial \phi} $$
$$ \frac{d}{dt} \mu r^2 \dot{\phi} = 0 $$
Angular momentum is conserved. We’ll need it later, so let’s call it \( l = \mu r^2 \dot{\phi} \). \( l \) can be solved by initial conditions, so we get a function for \( \dot{\phi}(r) \).
If we solve for \( r \) we get:
$$ \frac{d}{dt} \frac{\partial L}{\partial \dot{r}} = \frac{ \partial L}{\partial r} $$
$$ \frac{d}{dt} \mu \dot{r}^2 = \mu r \dot{\phi}^2 - \frac{dU}{dr} $$
This equation is just Newton’s second equation for a particle in one dimension with the standard potential and a fictitious outward centifugal force. \( F_c = \mu r \dot{\phi}^2 = \frac{l^2}{\mu r^3}\) (replacing \( \phi \)).
Effective Potential
Since the centrigufal force only depends on \( r \), we could instead wrap it into the potential as a new “effective potential”.
$$ U_{eff}(r) = U(r) + U_{cf}(r) = U(r) + \frac{l^2}{2 \mu r^2} $$
Then our equation or motion is just a particle moving in a single dimension with this effective potential.
Let’s plot it for our simulation!
Simulate
https://blog.c0nrad.io/sims/twobody/
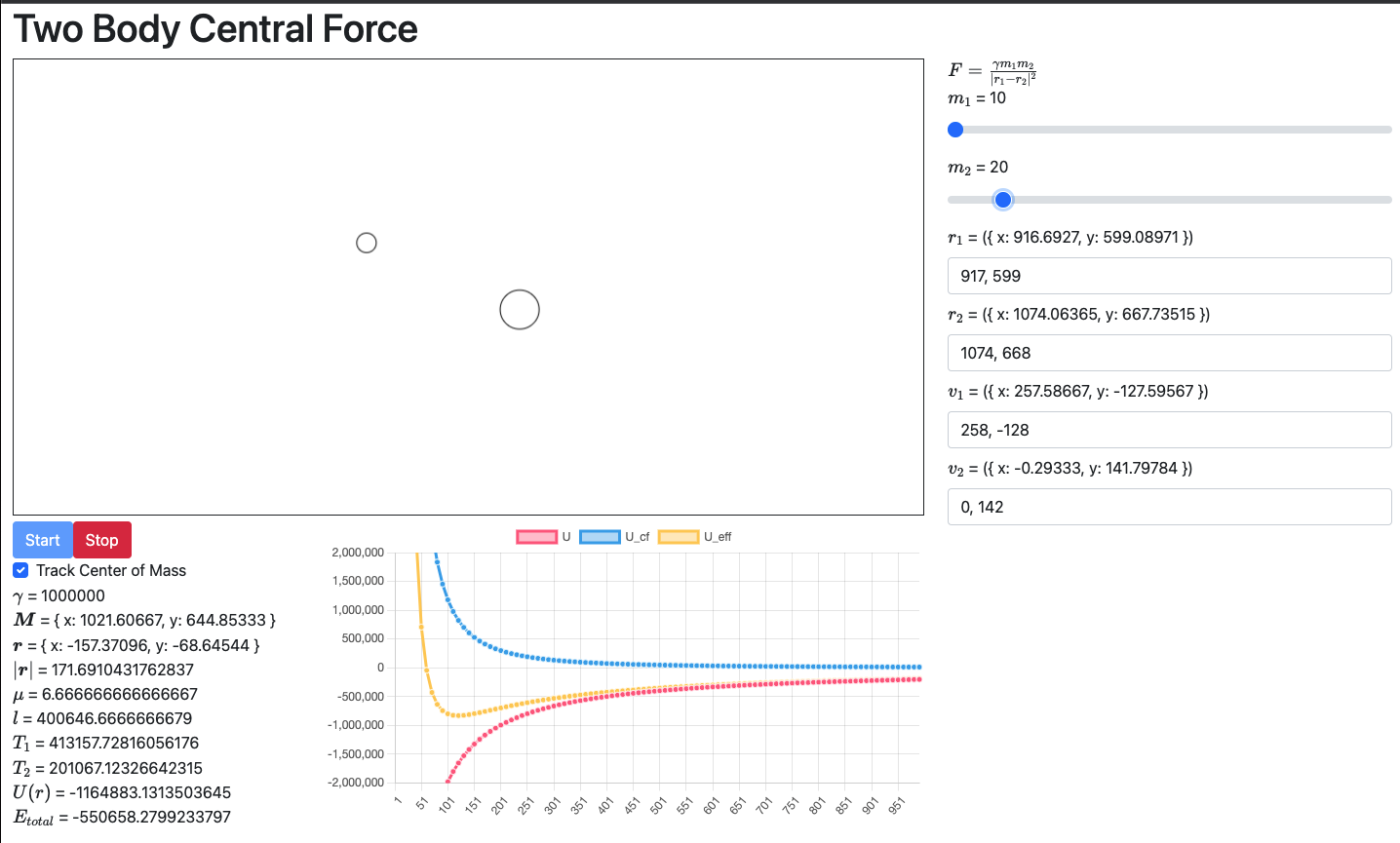
The effective plots are pretty fun. So the radius between the two bodies are around 100units with total energy of -550k. If you look at the yellow line in the plot you can see the potential valley it is stuck in.
A fun bug occurred!
It’s been awhile since I’ve had a tricky bug that I couldn’t immediately figure out. This one took maybe 3 hours over 2 days to figure out.
When I initially plotted the effective potential, it was saying the orbits were unstable at the radius the simulation was running at. But the simulation was running fine, it took awhile to prove myself that I was calculating everything correctly (I assumed for awhile that I was just calculating the angular momentum wrong).
Can you spot the bug?
The bug was around here…
The bug
The integrator was wrong in two different ways. First this.dt=10, so I should have been dividing by 1000 before updating the acceleration. And secondly I wasn’t even multiplying the velocity update by dt.
So yes, my orbits were actually unstable.
What went well
It was nice to actually run into an issue. Going through and proving to myself that all the math was correct was a good exercise.
Conclusion
Another fun exercise. Tomorrow we look at conic sections and other solutions to Kepler’s Problem.